Теория вероятностей (тервер) – раздел математики, который изучает случайные события и их свойства. Ознакомиться с ней нужно, чтобы понимать, как принимать взвешенные решения. Ведь зная статистические данные и анализируя закономерности, можно «предсказать» исход события.
Я не станут грузить вас сложными формулами – желающие углубленно заняться тервером могут сделать это по книге В. Е. Гмурмана «Теория вероятностей и математическая статистика». В статье покажу простые примеры для понимания зависимых и независимых событий, расскажу о состоянии неопределенности и интуитивном знании.
Материал полезен широкому кругу читателей.

Вероятность в зависимых событиях
Вы решаете отправить в подарок другу балык. Знаете номер дома, подъезд, этаж. Курьер просит называть номер квартиры. С мучительными усилиями вспоминаете, что в доме по три двери на площадку, но дальше – туман. Давайте рассчитаем, сможет ли курьер попасть в нужную квартиру с первого раза.
Имеем три варианта развития событий:
- Курьер звонит в первую (1) дверь.
- Курьер звонит во вторую (2) дверь.
- Курьер звонит в третью (3) дверь.
Но в истории участвует еще один человек: ваш друг. И событийность в его случае выглядит так:
- Друг за первой (1) дверью.
- Друг за второй (2) дверью.
- Друг за третьей (3) дверью.
Прежде чем пойти дальше, введем определение вероятности – количество благоприятных исходов к вероятному числу событий.
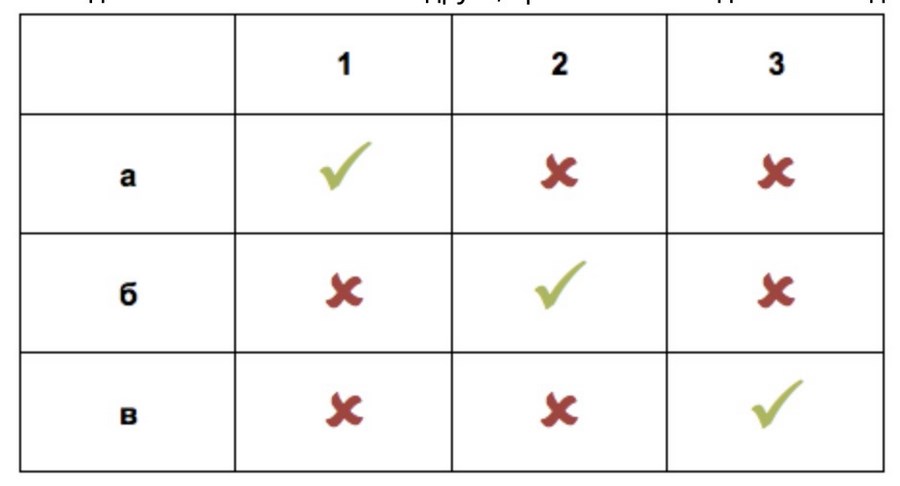
Теперь соберем данные в таблицу (таблица 1). Всего - 9 исходов. Отметим положительные (курьеру откроет друг) – их 3. Получается, что вероятность с первого раза позвонить в дверь к нужному человеку – 3/9 или 1/3. Если вам нравится видеть вероятность в процентах, умножьте результат на 100%.
Представим, что курьер ошибся, и за дверью оказалась сногсшибательная блондинка в коротком халате. Для курьера исход положительный, для вас – нет. Поэтому считаем новую вероятность:
- Курьер звонит в первую (1) квартиру.
- Курьер звонит во вторую (2) квартиру.
То же самое с другом:
- Друг ждет в первой (1) квартире.
- Друг ждет во второй (2) квартире.
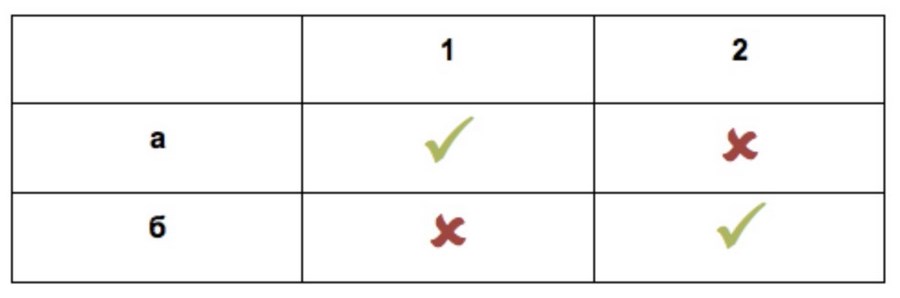
Теперь у нас 4 варианта и 2 – выигрышные (таблица 2). Вероятность со второго раза попасть в квартиру друга – 1/2. Она уменьшилась из-за зависимости событий: мы уже исключили неблагоприятный исход и расчёт нужно производить заново. Если курьер настолько невезуч, что промахнется во второй раз, вероятность попасть по адресу в третий раз – 100%. Опытным путем мы проверили, что за двумя предыдущими дверьми балык никто не ждет.
Пример с курьером — начальный уровень тервера. Он применим для бытовых нужд: предугадать вероятность побочного эффекта от антибиотиков, выбрать из разнообразия бабушкиных пирожков пирожок с повидлом и др.
На экзамене по теории вероятности советский математик и автор учебника Елена Вентцель спросила:
- Кому все понятно? Поднимите руки.
В аудитории живо взметнулся лес рук.
- Отлично! Остальные свободны, оценка – пять баллов! Поднявшие руки – останьтесь. За годы преподавания я так и не поняла большей части тервера. Рада, что вы мне все сейчас объясните.
Байка с математического факультета
У вас есть свой блог? Зарабатывайте с нами от 10 000 рублей на партнерской программе TeachLine.
Вероятность в независимых событиях
Независимые события не влияют друг на друга: количество благоприятных исходов в каждом новом событии не меняется.
Регина Тодоренко и Леся Никитюк в рамках программы «Орел и Решка» приехали в США. Обе хотят провести уик-энд «по богатому» и кидают монетку. Леся поставила на орла, Регина – на решку. Вероятность уехать на собственном авто у девушек одинакова: 1/2. На это раз повезло Лесе. Впрочем, как в следующей поездке тоже.

Теперь определим, могут ли независимые события происходить подряд с одним и тем же исходом. Лесе везло уже два раза и выпадал «орел». Повезет ли в третий раз? Составим список возможных исходов:
- Орел, орел, орел.
- Орел, орел, решка.
- Орел, решка, орел.
- Орел, решка, решка.
- Решка, орел, орел.
- Решка, орел, решка.
- Решка, решка, орел.
- Решка, решка, решка.
По результату видно: вероятность определенной последовательности каждый раз меньше на вероятность одного события. То есть вероятность определенной последовательности – произведение вероятностей каждого события. Если в одном событии вероятность 1/2, то в трех: 1/2*1/2*1/2=1/8.
Как человек принимает решения в состоянии неопределённости
Часть мозга, которая ответственна за оценку ситуации связана с медиаторной системой — центром мотивационных и эмоциональных процессов. Логика и эмоции часто конфликтуют между собой, поэтому решение принимается случайным образом.
У моей подруги аллергия на виноград. Но в студенчестве она не могла отказаться от бокала вина на вечеринке. Часто ее дерзость оставалась безнаказанной и организм нормально воспринимал аллерген. Реже протестовал: у подруги появлялись отеки на лице и в горле. В эти моменты ее левое полушарие отчаянно искало закономерность и просчитывало вероятность наступления аллергической реакции, правое же шептало: «Не пей, лицо распухнет!». Она могла вывести количество благоприятных исходов математическим путем и пить вино без опасений, но эмоции оказались сильней. Подруга раз и навсегда отказалась от любых продуктов с виноградом.
Хороший пример принятия решений описан в книге Млодинова «(Не) совершенная случайность». Допустим, вы отправили рассказ в четыре издательства. От каждого получили отказ. На эмоциях вы придете к мысли: рассказ ужасный! Хотя, если изучить биографии популярных писателей, может оказаться, что дело не в вас. Отказы в публикации получали Стивен Кинг, Джоан Роулинг, Виктор Франкл. Такие истории случались вовсе не из-за отсутствия у них дара: просто в одном издательстве редактор не понял тонкую философию автора, в другом – спешил домой и проставил визу не читая.
Почему интуитивное знание всегда противоречит статистике
Моя бабушка считает: в Албании убивают на каждом шагу. Хотя в стране она не была и новостей о не слышала: ей так кажется интуитивно. Наверняка и вы не раз испытывали подобное чувство. Оно называется интуитивное знание – внутреннее убеждение, что собственная оценка более правдива, чем официальные источники и статистика.

Классическое исследование на тему интуитивного знания провели Даниэль Канеман и Амос Тверский. Они дали задание группе студентов: на основании портрета, оценить утверждения с таблицы как более (1 балл) и менее (8 баллов) вероятные (таблица 3).
Портрет выглядел так: «Линда, возраст – немного за 30. Умная, говорит, что думает. В колледже изучала философию. Тогда же выступала против социального неравенства, дискриминации и использования ядерного оружия. Не замужем».
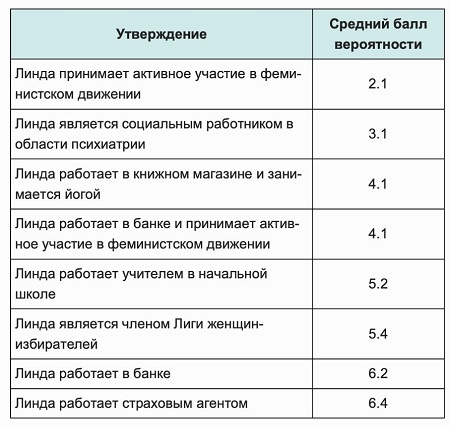
По портрету логично предположить, что Линда участвует в феминистском движении. Но студенты принимали решения интуитивно, что привело к ошибке. Вероятность, что Линда работает в банке и принимает участие в феминистском движении больше вероятности работы в банке.
Посмотрите на таблицу: вероятность работы в банке и увлечение феминистским движением – 4,1 балл. Но первое (работа в банке) и второе (феминистское движение) в сумме дают 8,3 балла. Согласно терверу, вероятность, что произойдут оба события не может быть выше, чем вероятность каждого события по отдельности. Главное утверждение (4,1 балла) содержит 2 события и является единым. В интуитивном решения правило тервера нарушено. Это доказывает — наши убеждения часто являются ложными.
В дальнейшем проводились множественные эксперименты, которые подтвердили догадку Канемана.
Вместо заключения
Теория вероятностей почти всегда разбивается о «случай», продиктованный убеждением или эмоцией отдельного человека. Поэтому использование ее в повседневной жизни может не оправдать ожиданий. Но выбирать вам! Хорошего дня!


